How to Count Divisible Pairs in an Array: A Quick Guide

In the programming world, counting the number of simpler structures in an object is an essential problem area. For example, counting combines that are divisible by a certain number in an array is one of the common problems.

The purpose is to build problem-solving skills and to further the knowledge about algorithms and data structure. This idea is familiar to solving competitive programming and coding interviews, where you have to find two elements in the given array, which in some way divide each other.

In this tutorial, different methods will be shown to solve this problem in Python from scratch and provide more efficient solutions in Python.

How to Count Divisible Pairs in an Array

Now it is time to look at the procedures to use to find the number of divisible integers by means of a given number. To count divisible pairs in an array, use the below methods:

Method 1: Brute Force Approach

The brute force approach involves checking each pair in the array to see if they are divisible by d. This could be done by iterating over all possible pairs and counting those that meet the condition.

This method is straightforward but can be inefficient for large arrays. This is done by using a sub-function to define all possible pairs and then count the number which satisfies the condition.

Let’s see an example:

1. First, iterate through each element in the array.
2. For each element, iterate through the remaining elements.
3. Then, check if the pair is divisible by the given number.
4. Finally, count the pairs that satisfy the condition.

Example:

def count_divisible_pairs(arr, k):
    count = 0
    n = len(arr)
    for i in range(n):
        for j in range(i + 1, n):
            if (arr[i] + arr[j]) % k == 0:
                count += 1
    return count

# Example usage
arr = [1, 2, 3, 4, 5]
k = 3
print(count_divisible_pairs(arr, k))  # Output: 4

Time Complexity: O(n^2)
This method can be easily understood and implemented it is simply wrong for big arrays as it entails nested loops. This method is straightforward but can be inefficient for large arrays because it involves nested loops.

Method 2: Using a Hash Map (Dictionary in Python)

A more effective approach involves using a hash map to store the remains of the elements when divided by the given number. This can be done because using a hash map allows checking the divisibility condition far more efficiently. This method reduces the time complexity significantly.

Let’s see an example:

1. First, create a hash map to store the remainder.
2. Then, iterate through the array and calculate the remainder of each element when divided by the given number.
3. Finally, the hash map is used to count pairs that satisfy the condition.

Example:

def count_divisible_pairs(arr, k):
    count = 0
    remainder_map = {}
    for num in arr:
        remainder = num % k
        complement = (k - remainder) % k
        if complement in remainder_map:
            count += remainder_map[complement]
        if remainder in remainder_map:
            remainder_map[remainder] += 1
        else:
            remainder_map[remainder] = 1
    return count

# Example usage
arr = [1, 2, 3, 4, 5]
k = 3
print(count_divisible_pairs(arr, k))  # Output: 4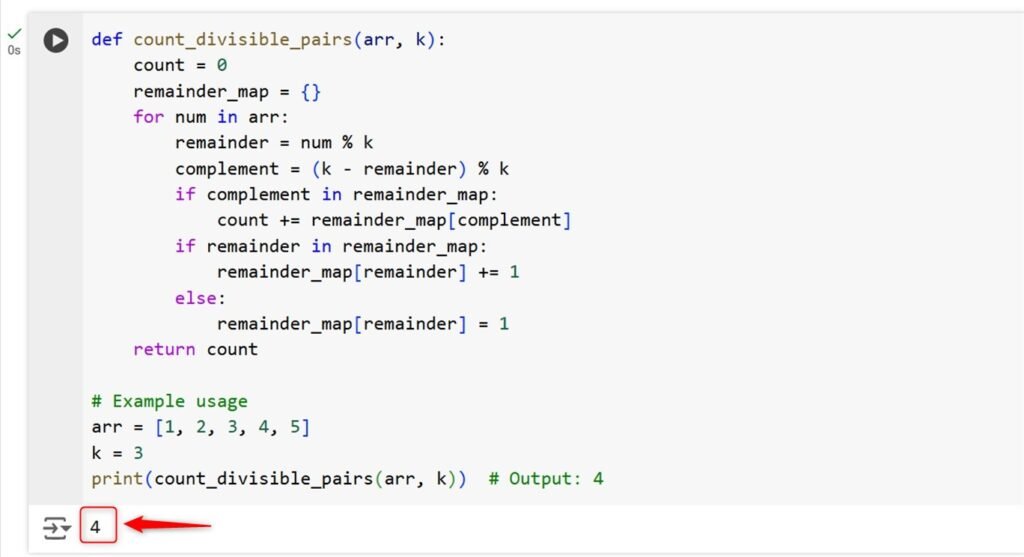

Time Complexity: O(n)
This method is highly efficient when compared to the brute force method where we use nested loops of loops. Nevertheless, it can still be optimized further.

Method 3: Sorting and Two Pointers Method

If the array is sorted, we can use two pointers to find the number of divisible pairs in a very optimal manner. This method can be efficient for certain types of input arrays.

Let’s see an example:

1. First, sort the array.
2. Then, two pointers were used to find pairs that satisfied the condition.
3. Finally, count the pairs.

Example:

def count_divisible_pairs(arr, k):
    arr.sort()
    count = 0
    left, right = 0, len(arr) - 1
    while left < right:
        if (arr[left] + arr[right]) % k == 0:
            count += 1
            left += 1
            right -= 1
        elif (arr[left] + arr[right]) < k:
            left += 1
        else:
            right -= 1
    return count

# Example usage
arr = [1, 2, 3, 4, 5]
k = 3
print(count_divisible_pairs(arr, k))  # Output: 2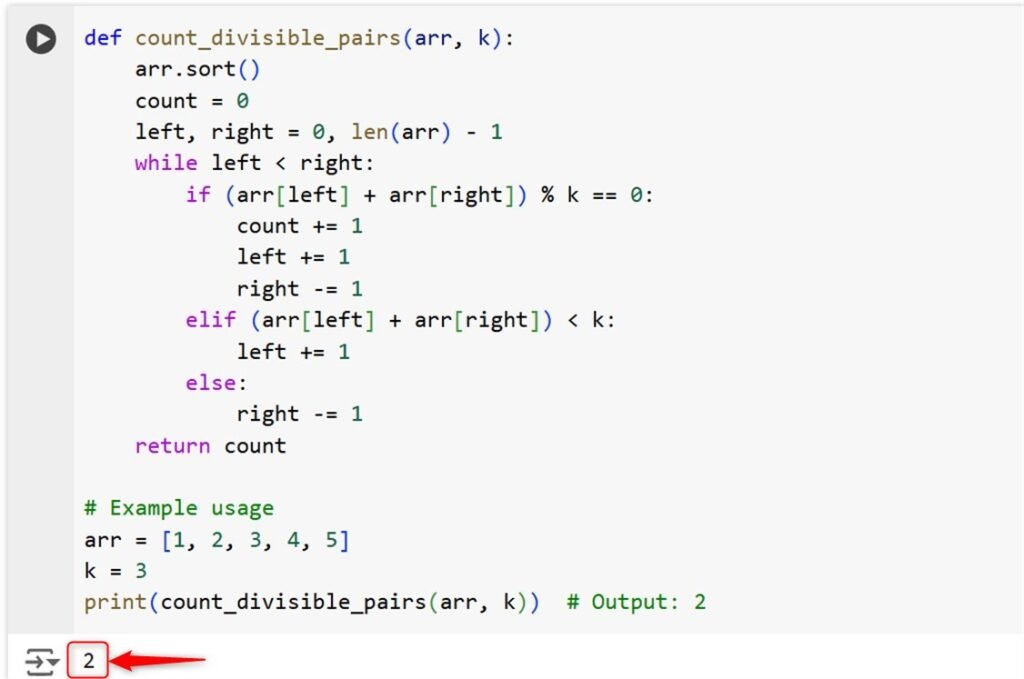

Time Complexity: O(n log n) for sorting + O(n)

Sorting takes O(n log n) plus O(n) about counting the frequency of a candidate element. This method reduces the time complexity by leveraging the sorted array property, but it comes at the cost of the initial sorting.

That is all from this guide.

Conclusion

Counting divisible pairs in an array can be approached in various ways, each method is most suitable for the other. The first method is straightforward but probably is not efficient when used on a large set of documents. The hash map method is slightly better than the brute force approach. In fact, sorting the array means more efficient searching algorithms, but, on the other hand, it indicates a preliminary sort. The decision that has to be made is what method should be applied in each case

Keep following the engrprogrammer.com for more guides.